統計的仮説検定
仮説検定(hypothesis testing)とは,関心のある仮説が発生事象に 因果関係があるかどうかを判定することである. ここで,仮説は標本の母集団の母数や確率分布である. 仮説検定の要点は,検証したい仮説と排他な仮説を設定して, これを検証し,関心のある仮説が成立するかを判断する. 数学で"何かが成立する"を証明する際に,"反例がある"と証明が成立しないのと同じ考えで, 排他な仮説の確率が高いということは,仮説に反例があるという確率が高いと判断して, 対象の仮説が成立しないと考える.
無帰仮説と対立仮説
仮説
仮説検定の仮説とは,標本の母集団の母数のことである. 通常,統計量を仮説として用いて,それを検定統計量(test statistic)という.
帰無仮説
帰無仮説(null hypothesis)は無価値な仮説という意味で, 検定したい仮説が成立するために,成立してほしくない仮説で, 帰無仮説が棄却することで,対象の仮説の正しさの確率を高める. 検定したい仮説を対立する仮説が採用される.\(H_0\)と表される.
対立仮説
対立仮説(alternative hypothesis)は帰無仮説と対立する仮説で, 帰無仮説が棄却したときに成立する仮説である.こちらが,興味のある対象の仮説になる. \(H_1\)と表される.
検定の設定
確率変数列 \(\{X_i\} _{i \in \mathbb{N} _+,i \leq n}\)を, 確率密度関数\(f _X(x:\theta)\)からの無作為標本とする. この確率密度関数のパラメータが属するパラメータ空間を\(\Theta\)とする. この空間を\(\Theta _1 = \Theta \backslash \Theta_0\)と分割する. ここで\(\theta \in \Theta _0\)となる仮説を帰無仮説として, \(H_0 : \theta \in \Theta _0\)と表し, \(\theta \in \Theta _1\)ととなる仮説を対立仮説とし,\(H_1 : \theta \in \Theta _1\)と表す. \(\Theta _0, \Theta _1\)が一つの要素(シングルトン)のときは,単純仮説(simple hypothesis)といい, 複数の要素から構成されるときは,複合仮説(composite hypothesis)という.
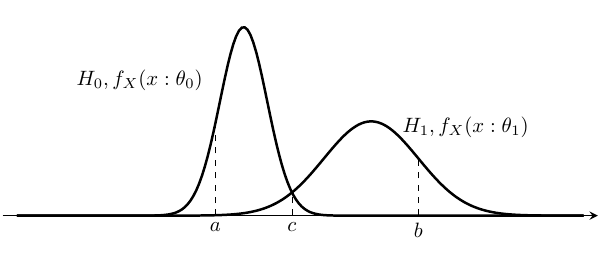
帰無仮説のパラメータに従う確率密度関数を \(f_X(x:\theta_0)\), 対立仮説のパラメータに従う確率密度関数を \(f_X(x:\theta_1)\)とする. ここで,標本\(X_i\)から\(\theta\)が,\(\Theta _0, \Theta _1\)どちらに属するかを判定する問題が仮説検定である.
上図で,標本\(X_i\)が\(a\)の位置にあるなら \(H_0\)を支持し,\(b\)の位置にあるなら \(H_1\)を支持し, \(c\)の位置にあるなら判定を保留したいと考えたい.しかし,仮説検定では判断を保留すると言う態度を取らない. 標本空間\(\Omega\)の中に集合\(R,A=\Omega \backslash R\)を設定し,\(X_i \in R\)である時 対立仮説が成立すると設定する.
仮説検定方式
仮説検定方式(hypothesis testing procedure)とは,標本空間\(\Omega\)を帰無仮説\(H_0\)を棄却(reject)する空間と,受容(accept)する空間に分割し,設定を行うことである. \[ R = \{x \in \Omega | H_0を棄却する \} \\ A = \Omega \backslash R = \{x \in \Omega | H_0を受容する \} \] \(R\)を\(H _0\)の棄却域(rejection region),\(A\)を\(H _0\)の受容域(acceptance region)と言う. \(R,A\)を決定する,標本\(\{X_i\} _{i \in \mathbb{N} _+,i \leq n}\)に基づいた統計量\(T=T(\mathbf{X})\)を検定統計量と言う.
検定関数
\[ \phi (\mathbf{X}) = I _R(\mathbf{X}) = \left \{ \begin{array}{ll} 1 & \mathbf{X} \in R \\ 0 & \mathbf{X} \not \in R \end{array} \right. \] と棄却域に関しての指示関数を検定関数(testing function)と言う.
設定された検出の評価
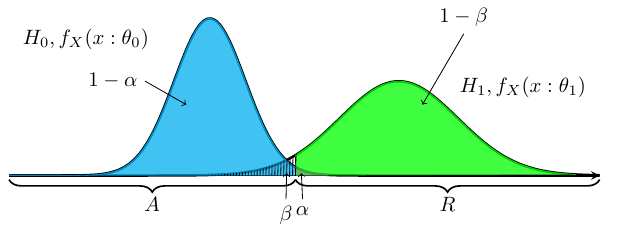
上の図にて,\(H_0:\theta_0\)の帰無仮説が正しいにもかかわらず, \(H_1:\theta_1\)の対立仮説が正しいと判断するという誤りを第一種の誤り(タイプ1エラー:type \({\rm I}\) error)という.第一種の誤りを犯す確率は,上図の\(\alpha\)が指す面積になる. \[ \alpha = P_{H_0}(X \in R:\theta_0) = \int _{R} f_X(x:\theta_0) dx \] 帰無仮説\(H_0\)が正しいときに帰無仮説\(H_0\)を棄却しない確率は, \[ 1 - \alpha = P _{H _0}(X \not \in R:\theta_0) \] と表され,\(\theta _0\)に対する信頼率(confidence level)という.
反対に,対立仮説\(H_1\)が正しいにもかかわらず,帰無仮説\(H_0\)が正しいと判断する誤りを第二種の誤り(タイプ2エラー:type \({\rm II}\) error)という. 第二種の誤りを犯す確率は,上図の\(\beta\)が指す面積になる. \[ \beta = P _{H _1}(X \not \in R:\theta_1) = \int _{R^c} f_X(x:\theta_1) dx \] 対立仮説\(H_1\)が正しいときに帰無仮説\(H_0\)を棄却する確率は, \[ 1-\beta = P _{H _1}(X \in R:\theta_1) \] と表され,\(\theta _1\)に対する検出力(power)という. 検出力を\(\theta\)の関数みなした時, \[ \beta(\theta) = 1-\beta = 1 - \int _{R^c} f_X(x:\theta) dx = \int _{R} f_X(x:\theta) dx \] を検出力関数(power function)という.
設定された仮説は,第一種の誤り,第二種の誤りがともに小さいほうが良い. まず,帰無仮説を棄却する時は,間違っていても低い確率で間違いたい. つまり,第一種の誤りが小さいほうが良い.第一種の誤りが小さいということは, 信頼率が高いということになる. そこで,まず第一種の誤り\(\alpha\)に対して,以下を満たすように,棄却域\(R\)を設定する. \[ \sup_{\theta \in \Theta_0} P(X \in R:\theta) \leq \alpha \]
この\(\alpha\)を有意水準(significance level)といい, 通常\(\alpha=0.05,\alpha=0.01\)となるように,\(R\)を設定する.
次に,第二種の誤り\(\beta\)を有意水準の範囲で小さくしたい. 有意水準\(\alpha\)の検定で,第二種の誤りが最も小さいものを, 有意水準\(\alpha\)の最強力検定(most powerful test)という.